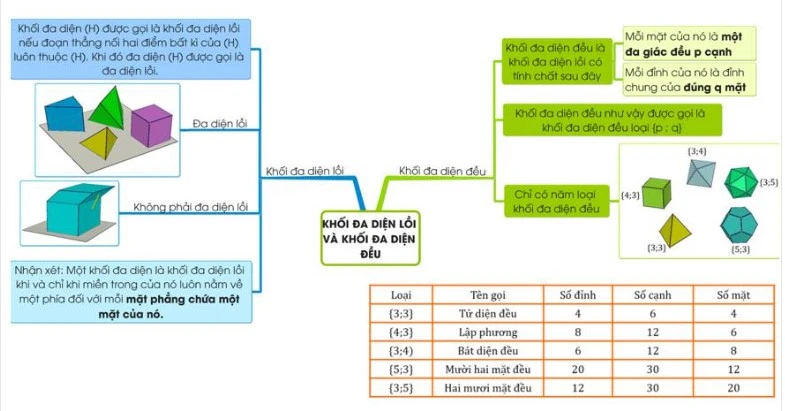
A. Lý thuyết khối đa diện lồi, khối đa diện đều
1. Khối đa diện lồi
a. Định nghĩa
Khối đa diện (H) được coi là khối đa diện lồi khi bất kỳ hai điểm nào trong khối đều có đoạn thẳng nối giữa chúng nằm hoàn toàn trong khối đó. Đặc điểm này đảm bảo rằng các góc bên trong của khối đều lớn hơn 180 độ và không có mặt nào bị lõm vào trong. Khối đa diện lồi là khái niệm cơ bản trong hình học không gian, thường được nghiên cứu trong các bài học toán học từ cơ bản đến nâng cao.
b. Ví dụ minh họa
Ví dụ về khối đa diện lồi bao gồm các hình khối như khối lập phương, khối tứ diện, và khối bát diện. Ngược lại, các hình khối như khối tứ giác lõm là ví dụ điển hình cho khối đa diện không lồi, nơi mà có ít nhất một đoạn nối không nằm trong khối.
c. Định lý Ơ-le
Định lý Ơ-le là một trong những định lý nổi bật trong lý thuyết khối đa diện lồi. Theo đó, trong mọi khối đa diện lồi, có một mối quan hệ giữa số đỉnh (D), số mặt (M) và số cạnh (C) được thể hiện qua công thức:
D - C + M = 2
Công thức này là một trong những công cụ quan trọng để xác định các thuộc tính của khối đa diện và nó thường được sử dụng để giải các bài toán liên quan đến hình học không gian.

2. Khối đa diện đều
a. Định nghĩa
Khối đa diện đều, ký hiệu là {p; q}, là một dạng khối đa diện lồi đặc biệt, trong đó:
- Mỗi mặt của khối đa diện là một đa giác đều có số cạnh là p.
- Mỗi đỉnh của khối đa diện là điểm chung của đúng q mặt.
Điều này có nghĩa là tất cả các mặt của khối đều giống nhau và cấu trúc của khối là rất đối xứng, tạo ra những hình khối tinh tế và đẹp mắt.
b. Ví dụ minh họa
Ví dụ về khối đa diện đều bao gồm khối lập phương {4;3}, khối tứ diện {3;3}, khối bát diện {3;4}, khối ngũ diện {5;3}, và khối thập diện {3;5}. Mỗi loại khối đa diện đều này có những đặc điểm riêng biệt làm cho nó trở thành một phần quan trọng trong các nghiên cứu về hình học không gian.
c. Định lý
Trong không gian, chỉ có 5 loại khối đa diện đều, được phân loại như sau:
- {3;3} - Tứ diện đều
- {4;3} - Khối lập phương
- {3;4} - Khối bát diện
- {5;3} - Khối ngũ diện
- {3;5} - Khối thập diện
Bảng dưới đây tóm tắt chi tiết các loại khối đa diện đều:
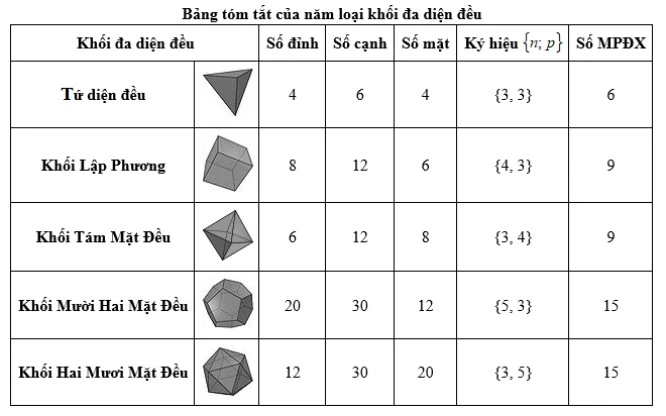
Nhận xét 1: Khối đa diện đều loại {n;p} có mối quan hệ giữa các yếu tố như sau: pD = 2C = nM.
Trong đó: D, C và M lần lượt là số đỉnh, số cạnh và số mặt của khối đa diện.
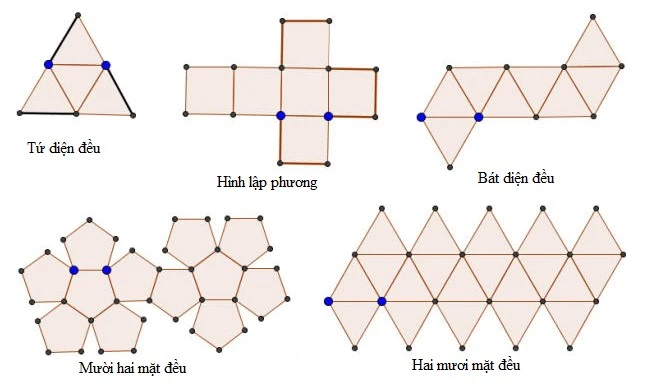
Nhận xét 2: Khi trải phẳng các khối đa diện đều, chúng ta sẽ thu được các hình vẽ 2D tương ứng với cấu trúc 3D của chúng.
Đăng ký ngay khóa học PAS THPT để được các thầy cô xây dựng lộ trình ôn tập toán thi THPT Quốc Gia ngay từ đầu năm học mới.


B. Sơ đồ tư duy bài khối đa diện lồi, khối đa diện đều


C. Những kết quả cần ghi nhớ
1. Một khối đa diện bất kỳ phải có ít nhất 4 mặt, 4 đỉnh và 6 cạnh.
2. Mỗi đỉnh của một khối đa diện bất kỳ phải là đỉnh chung của ít nhất 3 cạnh.
3. Không có khối đa diện lồi hay khối đa diện đều nào có 7 cạnh.
4. Một đa diện (H) có các cạnh của đa giác là p. Khi đó nếu (H) là lẻ thì p là số chẵn.
5. Một khối đa diện bất kỳ luôn luôn phân chia thành các khối tứ diện.
6. Khối đa diện có mặt là các tam giác thì tổng số mặt luôn là số chẵn.
7. Không tồn tại hình đa diện có số mặt lớn hơn hoặc bằng số cạnh, số đỉnh lớn hơn hoặc bằng số cạnh.
Với những kiến thức trên, các bạn có thể nắm vững các khái niệm và đặc điểm của khối đa diện lồi cũng như khối đa diện đều, từ đó áp dụng vào việc giải các bài toán hình học không gian hiệu quả hơn.

D. Bài tập vận dụng về khối đa diện lồi, khối đa diện đều
1. Dạng bài nhận biết khối đa diện lồi, khối đa diện đều
a. Phương pháp giải: Để giải bài tập dạng nhận biết khối đa diện, học sinh cần nhớ định nghĩa và các định lý liên quan đến khối đa diện lồi và khối đa diện đều. Việc nắm vững bảng tóm tắt các loại khối đa diện đều trong không gian cũng rất quan trọng.
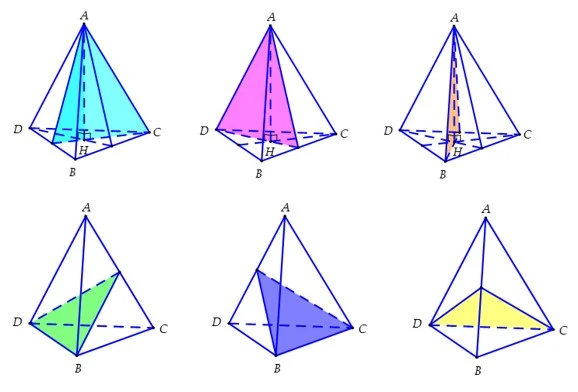
b. Ví dụ: Trong các hình dưới đây, hình nào không phải là khối đa diện lồi?
Đáp án: Hình 4 không phải là khối đa diện lồi vì theo định nghĩa, khối đa diện lồi yêu cầu đoạn thẳng nối giữa hai điểm bất kỳ phải nằm trong khối đó. Do đó, ở hình 4, đoạn MN không thỏa mãn điều kiện này.
2. Dạng bài các đặc điểm của khối đa diện đều
a. Phương pháp giải: Sử dụng các kiến thức đã học trong phần lý thuyết để xác định đặc điểm.
b. Bài tập vận dụng: Hỏi: Hình chóp 30 cạnh thì có bao nhiêu mặt?
Đáp án: 16 mặt.
Giải thích: Gọi a là số cạnh của đa giác đáy hình chóp. Do số cạnh đáy bằng số cạnh bên, ta có tổng số cạnh của hình chóp là 2a => 2a = 30 <=> a = 15.
Vậy đa giác đáy có 15 cạnh, số mặt bên của hình chóp là 15. Tuy nhiên, hình chóp có một mặt đáy nên tổng số mặt là 16.
3. Dạng bài xác định mặt phẳng đối xứng
a. Phương pháp giải: Dựa vào tính chất đối xứng, cần xác định các điểm đối xứng để tìm mặt phẳng đối xứng. Khi chọn một mặt phẳng đối xứng, cần đảm bảo rằng các điểm sẽ chia đều về hai phía.
b. Bài tập vận dụng: Hỏi: Tìm số mặt phẳng đối xứng của tứ diện đều.
Đáp án: Tứ diện đều có 6 mặt phẳng đối xứng.
Giải thích: Các mặt phẳng đối xứng của tứ diện đều chứa một cạnh và đi qua trung điểm của cạnh đối diện.

Để giải quyết mọi dạng bài tập về khối đa diện lồi và khối đa diện đều từ cơ bản đến nâng cao, các em hãy tham khảo khóa học PAS THPT ngay.
Hy vọng rằng qua bài viết trên, các em đã nắm vững kiến thức về khối đa diện lồi và khối đa diện đều cùng phương pháp giải các dạng bài tập thường gặp. Để học thêm nhiều kiến thức toán học 12 và các môn học khác, hãy truy cập trang web của VUIHOC nhé! Chúc các em học tập hiệu quả và tràn đầy niềm vui!
>> Mời các bạn xem thêm:
- Khái niệm về khối đa diện
- Bất phương trình mũ và bất phương trình lôgarit
- Lý thuyết về mặt tròn xoay













